Tutorial on the Elpi programming language
| Author: | Enrico Tassi |
|---|
This little tutorial does not talk about Coq, but rather focuses on
Elpi as a programming language. It assumes no previous knowledge of
Prolog, λProlog or Elpi. Coq is used as an environment for stepping trough
the tutorial one paragraph at a time. The text between lp:{{ and }} is
Elpi code, while the rest are Coq directives to drive the Elpi interpreter.
Logic programming
Elpi is a dialect of λProlog enriched with constraints. We start by introducing the first order fragment of λProlog, i.e. the terms will not contain binders. Later we cover terms with binders and constraints.
Our first program is called tutorial.
We begin by declaring the signature of our terms.
Here we declare that person is a type, and that
mallory, bob and alice are terms of that type.
Elpi Program tutorial lp:{{
kind person type.
type mallory, bob, alice person.
}}.An Elpi program is made of rules that declare when predicates hold and that are accumulated one after the other. Rules are also called clauses in Prolog's slang, so we may use both terms interchangeably.
The next code snippet accumulates on top
of the current tutorial program a predicate declaration for age
and three rules representing our knowledge about our terms.
Elpi Accumulate lp:{{
pred age o:person, o:int.
age mallory 23.
age bob 23.
age alice 20.
}}.The predicate age has two arguments, the former is a person while
the latter is an integer. The label o: (standing for output)
is a mode declaration, which we will explain later (ignore it for now).
Note
int is the built-in data type of integers
Integers come with usual arithmetic operators, see the calc built-in.
In order to run our program we have to write a query, i.e. a predicate expression containing variables such as:
age alice A
The execution of the program is expected to assign a value to A, which
represents the age of alice.
Important
Syntactic conventions:
- variables are identifiers starting with a capital letter, eg
A,B,FooBar,Foo_bar,X1 - constants (for individuals or predicates) are identifiers
starting with a lowercase letter, eg
foo,bar,this_that,camelCase,dash-allowed,qmark_too?,arrows->and.dots.as<-well
A query can be composed of many predicate expressions separated by ,
that stands for conjunction: we want to get an answer to all the
predicate expressions.
coq.say is a built-in predicate provided by Coq-Elpi which
prints its arguments.
You can look at the output buffer of Coq to see the value for A or hover
or toggle the little bubble after }}. if you are reading the tutorial with a
web browser.
Note
string is a built-in data type
Strings are delimited by double quotes and \ is the escape symbol.
The predicate age represents a relation (in contrast to a function)
and it computes both ways: we can ask Elpi which person P is 23 years old.
Unification
Operationally the query age P 23 is unified with each
and every rule present in the program starting from the first one.
Unification compares two terms structurally and eventually assigns variables. For example for the first rule of the program we obtain the following unification problem:
age P 23 = age mallory 23
This problem can be simplified into smaller unification problems following the structure of the terms:
age = age P = mallory 23 = 23
The first and last are trivial, while the second one can be satisfied by
assigning mallory to P. All equations are solved,
hence unification succeeds.
See also the Wikipedia page on Unification.
Since the first part of the query is successful the rest of
the query is run: the value of P is printed as well as
the "is 23 years old" string.
Note
= is a regular predicate
The query age P 23 can be also written as follows:
A = 23, age P A, Msg = "is 23 years old", coq.say P Msg
Let's try a query harder to solve!
This time the unification problem for the first rule in the program is:
age P 20 = age mallory 23
that is simplified to:
age = age P = mallory 20 = 23
The second equation can be solved by assigning mallory to P,
but the third one has no solution, so unification fails.
Backtracking
When failure occurs all assignments are undone (i.e. P is unset again)
and the next rule in the program is tried. This operation is called
backtracking.
The unification problem for the next rule is:
age P 20 = age bob 23
This one also fails. The unification problem for the last rule is:
age P 20 = age alice 20
This one works, and the assignment P = alice is kept as the result
of the first part of the query. Then P is printed and the program
ends.
An even harder query is the following one where we ask for two distinct individuals to have the same age.
This example shows that backtracking is global. The first solution for
age P A and age Q A picks P and Q to
be the same individual mallory,
but then not(P = Q) fails and forces the last choice that was made to be
reconsidered, so Q becomes bob.
Look at the output of the following code to better understand how backtracking works.
Note
not is a black hole
The not(P) predicate tries to solve the query P: it fails if
P succeeds, and succeeds if P fails. In any case no trace is left
of the computation for P. E.g. not(X = 1, 2 < 1) succeeds, but
the assignment for X is undone. See also the section
about the foundations of λProlog.
Facts and conditional rules
The rules we have seen so far are facts: they always hold. In general rules can only be applied if some condition holds. Conditions are also called premises, we may use the two terms interchangeably.
Here we add to our program a rule that defines what older P Q means
in terms of the age of P and Q.
Note
:- separates the head of a rule from the premises
Elpi Accumulate lp:{{
pred older o:person, o:person.
older P Q :- age P N, age Q M, N > M.
}}.The rule reads: P is older than Q if
N is the age of P
and M is the age of Q
and N is greater than M.
Let's run a query using older:
The query older bob X is unified with the head of
the program rule older P Q
assigning P = bob and X = Q. Then three new queries are run:
age bob N age Q M N > M
The former assigns N = 23, the second one first
sets Q = mallory and M = 23. This makes the last
query to fail, since 23 > 23 is false. Hence the
second query is run again and again until Q is
set to alice and M to 20.
Variables in the query are said to be existentially quantified because Elpi will try to find one possible value for them.
Conversely, the variables used in rules are universally quantified in the front of the rule. This means that the same program rule can be used multiple times, and each time the variables are fresh.
In the following example the variable P in older P Q :- ...
once takes bob and another time takes mallory.
Predicates v.s. functions
It is often the case that predicates are intended to describe functions, i.e. associate only one "output" to a given "input".
Elpi Program tutorial_functions lp:{{
kind person type.
type mallory, bob, alice person.
func age person -> int.
age mallory 23.
age bob 23.
age alice 20.
}}.The function declaration for age separates the domain of the function
from the codomain with the -> symbol: the function associates to each
person a single age (or fail if the person has no rule for it).
After this declaration Elpi refuses to add rules that would break this property:
In this case it is easy to tell that the two rules overlap: both
apply to a query like age mallory A.
In general is not possible to decide if two rules really overlap. For example this legit function is rejected.
In order to accept this function Elpi would need to deduce that 16 is not
a prime number, and also deduce that prime is really implementing a
primality test (like proving its code correct, or at least that it would fail
on 16).
In order to have the code accepted by Elpi, as a function, one has to use
the cut operator ! to enforce the following operational reading to the
rules: when the cut operator is reached the other rules are discarded.
Elpi Program tutorial_functions3 lp:{{
func prime int -> . % code omitted
func f int -> int.
f X Y :- prime X, !, Y = 2.
f 16 Y :- Y = 4.
}}.Elpi accepts the code because:
- the two rules are mutually esclusive (thanks to the cut)
- because the code after the cut is itself a function call
(
Y = 2is a call to unification that is a function)
The following code is rejected because the second condition does not hold.
Since one_or_two can produce many results, also f can.
At the same time the code below is accepted.
Elpi Program tutorial_functions5 lp:{{
func prime int -> .
pred one_or_two o:int.
one_or_two 1.
one_or_two 2.
func f int -> int.
f X Y :- one_or_two Y, !, prime X.
f 16 Y :- Y = 4.
}}.The reson why it is accepted is because, operationally, the cut
operator does not only discard the other rules for the current predicated,
but also the (yet to be used) rules for all the predicates that preceeds it.
In this case one_or_two's second rule would be discarded, turning the
predicate call one_or_two Y into a "function" call (committing to the
first result given by the predicate one_or_two).
Modes and matching
The syntax
func age person -> int.
desugars to
:functional % this is an attribute (a special comment) pred age i:person, o:int.
that asserts two things. First age is expected to behave like a function.
Second its first argument is flagged with the input mode.
Query arguments in input mode are matched against the rule's corresponding argument that we call a pattern. The difference w.r.t. unification is that only variables occurring in the pattern can be assigned. Matching is not symmetric: the pattern and the query argument play different roles, in particular the query argument can only be inspected (destructed) by the pattern, and never assigned (constructed). For example:
The query fails because P (occurring in the query)
does not match bob nor mallory: there is no way to
make P = bob hold without assigning P but that is forbidden by
the i: directive in the signature of age.
Note
Pattern matching API
As unification is available via the (=), pattern matching is available via pattern_match.
f 1 = f X % ok f X = f 1 % ok pattern_match (f X) (f 1) % ok pattern_match (f 1) (f X) % ko (the pattern is the first argument)
The only drawback of marking the first argument of age as an imput
is that it will prevent to use the predicate in the other direction, e.g. to
find any person of age 23. For that one would need a different predicate,
since Elpi does not support multiple signatures for the same symbol.
We often use the R suffix to denote the non-function version of a predicate,
for example see std.append and std.appendR.
Terms with binders
So far the syntax of terms is based on constants
(eg age or mallory) and variables (eg X).
λProlog adds another term constructor:
λ-abstraction (written x\ ...).
Note
the variable name before the \ can be a capital
Given that it is explicitly bound Elpi needs not to guess if it is a global symbol or a rule variable (that required the convention of using capitals for variables in the first place).
λ-abstraction
Functions built using λ-abstraction can be applied to arguments and honor the usual β-reduction rule (the argument is substituted for the bound variable).
In the following example F 23 reads, once
the β-reduction is performed, age alice 23.
Let's now write the "hello world" of λProlog: an
interpreter and type checker for the simply
typed λ-calculus. We call this program stlc.
We start by declaring that term is a type and
that app and fun are constructors of that type.
Elpi Program stlc lp:{{
kind term type.
type app term -> term -> term.
type fun (term -> term) -> term.
}}.The constructor app takes two terms
while fun only one (of functional type).
Note that
- there is no constructor for variables, we will use the notion of bound variable of λProlog in order to represent variables
funtakes a function as subterm, i.e. something we can build using the λ-abstractionx\ ...
As a consequence, the identity function λx.x is written like this:
fun (x\ x)
while the first projection λx.λy.x is written:
fun (x\ fun (y\ x))
Another consequence of this approach is that there is no such thing as a free variable in our representation of the λ-calculus. Variables are only available under the λ-abstraction of the programming language, that gives them a well defined scope and substitution operation (β-reduction).
This approach is called HOAS.
We can now implement weak head reduction, that is we stop reducing
when the term is a fun or a global constant (potentially applied).
If the term is app (fun F) A then we compute the reduct F A.
Note that F is a λProlog function, so passing an argument to it
implements the substitution of the actual argument for the bound variable.
We first give a type and a mode for our predicate whd. It reads
"whd takes a term in input and gives a term in output". We will
explain what input means precisely later, for now just think about it
as a comment.
Elpi Accumulate lp:{{
pred whd i:term, o:term.
% when the head "Hd" of an "app" (lication) is a
% "fun" we substitute and continue
whd (app Hd Arg) Reduct :- whd Hd (fun F), !,
whd (F Arg) Reduct.
% otherwise a term X is already in normal form.
whd X Reduct :- Reduct = X.
}}.Recall that, due to backtracking, all rules are potentially used. Here whenever the first premise of the first rule succeeds we want the second rule to be skipped, since we found a redex.
The premises of a rule are run in order and the ! operator discards all
other rules following the current one. Said otherwise it commits to
the currently chosen rule for the current query (but leaves
all rules available for subsequent queries, they are not erased from the
program). So, as soon as whd Hd (fun F) succeeds we discard the second
rule.
Another little test using global constants:
Elpi Accumulate lp:{{ type foo, bar term. }}.
A last test with a lambda term that has no weak head normal form:
Elpi Bound Steps 1000. (* Let's be cautious *)Elpi Bound Steps 0.
pi x\ and ==>
We have seen how to implement substitution using the binders of λProlog. More often than not we need to move under binders rather than remove them by substituting some term in place of the bound variable.
In order to move under a binder and inspect the body of a function λProlog
provides the pi quantifier and the ==> connective.
A good showcase for these features is to implement a type checker for the simply typed lambda calculus. See also the Wikipedia page on the simply typed lambda calculus.
We start by defining the data type of simple types.
We then declare a new predicate of (for "type of") and finally
we provide two rules, one for each term constructor.
Elpi Accumulate lp:{{
kind ty type. % the data type of types
type arr ty -> ty -> ty. % our type constructor
pred of i:term, o:ty. % the type checking algorithm
% for the app node we ensure the head is a function from
% A to B, and that the argument is of type A
of (app Hd Arg) B :-
of Hd (arr A B), of Arg A.
% for lambda, instead of using a context (a list) of bound
% variables we use pi and ==> , explained below
of (fun F) (arr A B) :-
pi x\ of x A ==> of (F x) B.
}}.The pi name\ code syntax is reserved, as well as
rule ==> code.
Operationally pi x\ code introduces a fresh
constant c for x and then runs code.
Operationally rule ==> code adds rule to
the program and runs code. Such extra rule is
said to be hypothetical.
Both the constant for x and rule are
removed once code terminates.
Important
hypothetical rules are added at the top of the program
Hypothetical rules hence take precedence over static rules, since they are tried first.
Note that in this last example the hypothetical rule is going to be
of c A for a fixed A and a fresh constant c.
The variable A is fixed but not assigned yet, meaning
that c has a type, and only one, but we may not know it yet.
Now let's assign a type to λx.λy.x:
Let's run this example step by step:
The rule for fun is used:
arrow A1 B1is assigned toTyby unification- the
pi x\quantifier creates a fresh constantc1to play the role ofx - the
==>connective adds the ruleof c1 A1the program - the new query
of (fun y\ c1) B1is run.
Again, the rule for fun is used (since its variables are
universally quantified, we use A2, B2... this time):
arrow A2 B2is assigned toB1by unification- the
pi x\quantifier creates a fresh constantc2to play the role ofx - the
==>connective adds the ruleof c2 A2the program - the new query
of c1 B2is run.
The (hypothetical) rule of c1 A1 is used:
- unification assigns
A1toB2
The value of Ty is hence arr A1 (arr A2 A1), a good type
for λx.λy.x (the first argument and the output have the same type A1).
What about the term λx.(x x) ?
The ; infix operator stands for disjunction. Since we see the message
of failed: the term fun (x\ app x x) is not well typed.
First, the rule for elpi:fun is selected:
arrow A1 B1is assigned toTyby unification- the
pi x\quantifier creates a fresh constantc1to play the role ofx - the
==>connective adds the ruleof c1 A1the program - the new query
of (app c1 c1) B1is run.
Then it's the turn of typing the application:
the query
of c1 (arr A2 B2)assigns toA1the valuearr A2 B2. This means that the hypothetical rule is nowof c1 (arr A2 B2).the query
of c1 A2fails because the unificationof c1 A2 = of c1 (arr A2 B2)
has no solution, in particular the sub problem
A2 = (arr A2 B2)fails the so called occur check.
Logical foundations
This section tries to link, informally, λProlog with logic, assuming the reader has some familiarity with first order intuitionistic logic and proof theory. The reader which is not familiar with that can probably skip this section, although section functional-style contains some explanations about the scope of variables which are based on the logical foundations of the language.
The semantics of a λProlog program is given by interpreting it in terms of logical formulas and proof search in intuitionistic logic.
A rule
p A B :- q A C, r C B.
has to be understood as a formula
A query is a goal that is proved by backchaining
rules. For example p 3 X
is solved by unifying it with the conclusion of
the formula above (that sets A to 3) and
generating two new goals, q 3 C and
r C B. Note that C is an argument to both
q and r and acts as a link: if solving q
fixes C then the query for r sees that.
Similarly for B, that is identified with X,
and is hence a link from the solution of r to
the solution of p.
A rule like:
of (fun F) (arr A B) :- pi x\ of x A ==> of (F x) B.
reads, as a logical formula:
where \(F\) stands for a function. Alternatively, using the inference rule notation typically used for type systems:
Hence, x and of x A are available only
temporarily to prove of (F x) B and this is
also why A cannot change during this sub proof (A is
quantified once and forall outside).
Each program execution is a proof (tree) of the query and is made of the program rules seen as proof rules or axioms.
As we hinted before negation is a black hole, indeed the usual definition of \(\neg A\) as \(A \to \bot\) is the one of a function with no output (see also the the Wikipedia page on the Curry-Howard correspondence).
Constraints
Elpi extends λProlog with syntactic constraints and rules to manipulate the store of constraints.
Syntactic constraints are goals suspended on a variable which are resumed as soon as that variable gets instantiated. While suspended they are kept in a store which can be manipulated by dedicated rules.
A companion facility is the declaration of modes. The argument of a predicate can be marked as input to avoid instantiating the goal when it is unified with the head of a rule (an input argument is matched, rather than unified).
A simple example: Peano's addition:
Elpi Program peano lp:{{ kind nat type. type z nat. type s nat -> nat. pred add o:nat, o:nat, o:nat. add (s X) Y (s Z) :- add X Y Z. add z X X. }}.
Unfortunately the relation does not work well
when the first argument is a variable. Depending on the
order of the rules for add Elpi can either diverge or pick
z as a value for X (that may not be what one wants)
Elpi Bound Steps 100.Elpi Bound Steps 0.
Indeed the first rule for add can be applied forever.
If one exchanges the two rules in the program, then Elpi
terminates picking z for X.
We can use the mode directive in order to
match arguments marked as i: against the patterns
in the head of rules, rather than unifying them.
Elpi Program peano2 lp:{{ kind nat type. type z nat. type s nat -> nat. pred sum i:nat, i:nat, o:nat. sum (s X) Y (s Z) :- sum X Y Z. sum z X X. sum _ _ _ :- coq.error "nothing matched but for this catch all clause!". }}.
The query fails because no rule first argument matches X.
Instead of failing we can suspend goals and turn them into syntactic constraints
Elpi Program peano3 lp:{{ kind nat type. type z nat. type s nat -> nat. func sum nat, nat -> nat. sum (s X) Y (s Z) :- !, sum X Y Z. sum z X X :- !. sum X Y Z :- % the head of the rule always unifies with the query, so % we double check X is a variable (we could also be % here because the other rules failed) var X, % then we declare the constraint and schedule its resumption % on the assignment of X declare_constraint (sum X Y Z) [X]. }}.
Syntactic constraints are resumed when the variable they are suspended on is assigned:
Here a couple more examples. Keep in mind that:
- resumption can cause failure
- recall that
;stands for disjunction
In this example the computation suspends, then makes progress, then suspends again...
Sometimes the set of syntactic constraints becomes unsatisfiable and we would like to be able to fail early.
Elpi Accumulate lp:{{ func even nat. func odd nat. even z :- !. even (s X) :- !, odd X. odd (s X) :- !, even X. odd X :- var X, declare_constraint (odd X) [X]. even X :- var X, declare_constraint (even X) [X]. }}.
Constraint Handling Rules
A constraint (handling) rule can see the store of syntactic constraints as a whole, remove constraints and/or create new goals:
Elpi Accumulate lp:{{ constraint even odd { % if two distinct, conflicting, constraints about the same X % are part of the constraint store rule (even X) (odd X) <=> % generate the following goal (coq.say X "can't be even and odd at the same time", fail). } }}.
Note
fail is a predicate with no solution
See also the Wikipedia page on Constraint Handling Rules for an introduction to the sub language to manipulate constraints.
Functional style
Elpi is a relational language, not a functional one. Still some features typical of functional programming are available, with some caveats.
Spilling (relation composition)
Chaining "relations" can be painful, especially when they look like functions. Here we use std.append and std.rev to build a palindrome:
Elpi Program function lp:{{ pred make-palindrome i:list A, o:list A. make-palindrome L Result :- std.rev L TMP, std.append L TMP Result. }}.
The make-palindrome predicate has to use a temporary variable
just to pass the output of a function as the input to another function.
Spilling is a syntactic elaboration which does that for you.
Expressions between { and } are
said to be spilled out and placed just before the predicate
that contains them.
Elpi Accumulate lp:{{ pred make-palindrome2 i:list A, o:list A. make-palindrome2 L Result :- std.append L {std.rev L} Result. }}.
The two versions of make-palindrome are equivalent.
Actually the latter is elaborated into the former.
APIs for built-in data
Functions about built-in data types are available via the
calc predicate or its infix version is. Example:
The calc predicate works nicely with spilling:
Allocation of variables
The language lets one use λ-abstraction also to write anonymous rules but one has to be wary of where variables are bound (allocated really).
In our example we use the higher order predicate std.map:
pred std.map i:list A, i:(A -> B -> prop), o:list B.
Note
prop is the type of predicates
The actual type of the std.map symbol is:
type std.map list A -> (A -> B -> prop) -> list B -> prop.
The pred directive complements a type declaration for predicates
(the trailing -> prop is implicit) with a mode declaration for
each argument.
The type of the second argument of std.map
is the one of a predicate relating A with B.
Let's try to call std.map passing an anonymous rule (as we
would do in a functional language by passing an anonymous function):
Elpi Accumulate lp:{{ pred bad i:list int, o:list int. bad L Result :- std.map L (x\ r\ TMP is x + 1, r = TMP) Result. pred good i:list int, o:list int. good L Result :- std.map L good.aux Result. good.aux X R :- TMP is X + 1, R = TMP. pred good2 i:list int, o:list int. good2 L Result :- std.map L (x\ r\ sigma TMP\ TMP is x + 1, r = TMP) Result. }}.
The problem with bad is that TMP is fresh each time the rule
is used, but not every time the anonymous rule passed to map
is used. Technically TMP is quantified (allocated) where L
and Result are.
There are two ways to quantify TMP correctly, that is inside the
anonymous predicate. One is to actually name the predicate. Another one is
to use the sigma x\ quantifier to allocate TMP at every call.
We recommend to name the auxiliary predicate.
Tip
predicates whose name ends in .aux don't trigger a missing type
declaration warning
One last way to skin the cat is to use ==> as follows. It gives us
the occasion to clarify further the scope of variables.
Elpi Accumulate lp:{{ pred good3 i:list int, o:list int. good3 L Result :- pi aux\ (pi TMP X R\ aux X R :- TMP is X + 1, R = TMP) ==> std.map L aux Result. }}.
In this case the auxiliary predicate aux
is only visible inside good3.
What is interesting to remark is that the quantifications are explicit
in the hypothetical rule, and they indicate clearly that each and every
time aux is used TMP, X and R are fresh.
The pi x\ quantifier is dual to sigma x\ : since here it
occurs negatively it has the same meaning. That is, the hypothetical rule
could be written pi X R\ aux X R :- sigma TMP\ TMP is X + 1, R = TMP.
Tip
pi x\ and sigma x\ can quantify on a bunch of variables
at once
That is, pi x y\ ... is equivalent to pi x\ pi y\ ... and
sigma x y\ ... is equivalent to sigma x\ sigma y\ ....
Tip
==> can load more than one clause at once
It is sufficient to put a list on the left hand side, eg [ rule1, rule2 ] ==> code.
Moreover one can synthesize a rule before loading it, eg:
Rules = [ one-more-rule | ExtraRules ], Rules ==> code
The last remark worth making is that bound variables are intimately related to universal quantification, while unification variables are related to existential quantification. It goes without saying that the following two formulas are not equivalent and while the former is trivial the latter is in general false:
Let's run these two corresponding queries:
Another way to put it: x is in the scope of Y only in the first
formula since it is quantified before it. Hence x can be assigned to
Y in that case, but not in the second query, where it is quantified
after.
More in general, λProlog tracks the bound variables that are in scope of each unification variable. There are only two ways to put a bound variable in the scope:
quantify the unification variable under the bound one (first formula)
pass the bound variable to the unification variable explicitly: in this case the unification variable needs to have a functional type. Indeed \(\exists Y, \forall x, (Y x) = x\) has a solution:
Ycan be the identity function.
If we look again at the rule for type checking λ-abstraction:
of (fun F) (arr A B) :- pi x\ of x A ==> of (F x) B.
we can see that the only unification variable that sees the fresh
x is F, because we pass x to F explicitly
(recall all unification variables such as F, A, B are
quantified upfront, before the pi x\ ).
Indeed when we write:
on paper, the variable denoted by x being bound there can only occur in
\(f\), not in \(\Gamma\) or \(B\) for example (although a
different variable could be named the same, hence the usual freshness side
conditions which are not really necessary using HOAS).
Remark that in the premise the variable \(x\) is still bound, this time
not by a λ-abstraction but by the context \(\Gamma, x : A\).
In λProlog the context is the set of hypothetical rules and pi\
-quantified variables and is implicitly handled by the runtime of the
programming language.
A slogan to keep in mind is that:
Important
There is no such thing as a free variable!
Indeed the variable bound by the λ-abstraction (of our data) is replaced by a fresh variable bound by the context (of our program). This is called binder mobility. See also the paper Mechanized metatheory revisited by Dale Miller which is an excellent introduction to these concepts.
Debugging
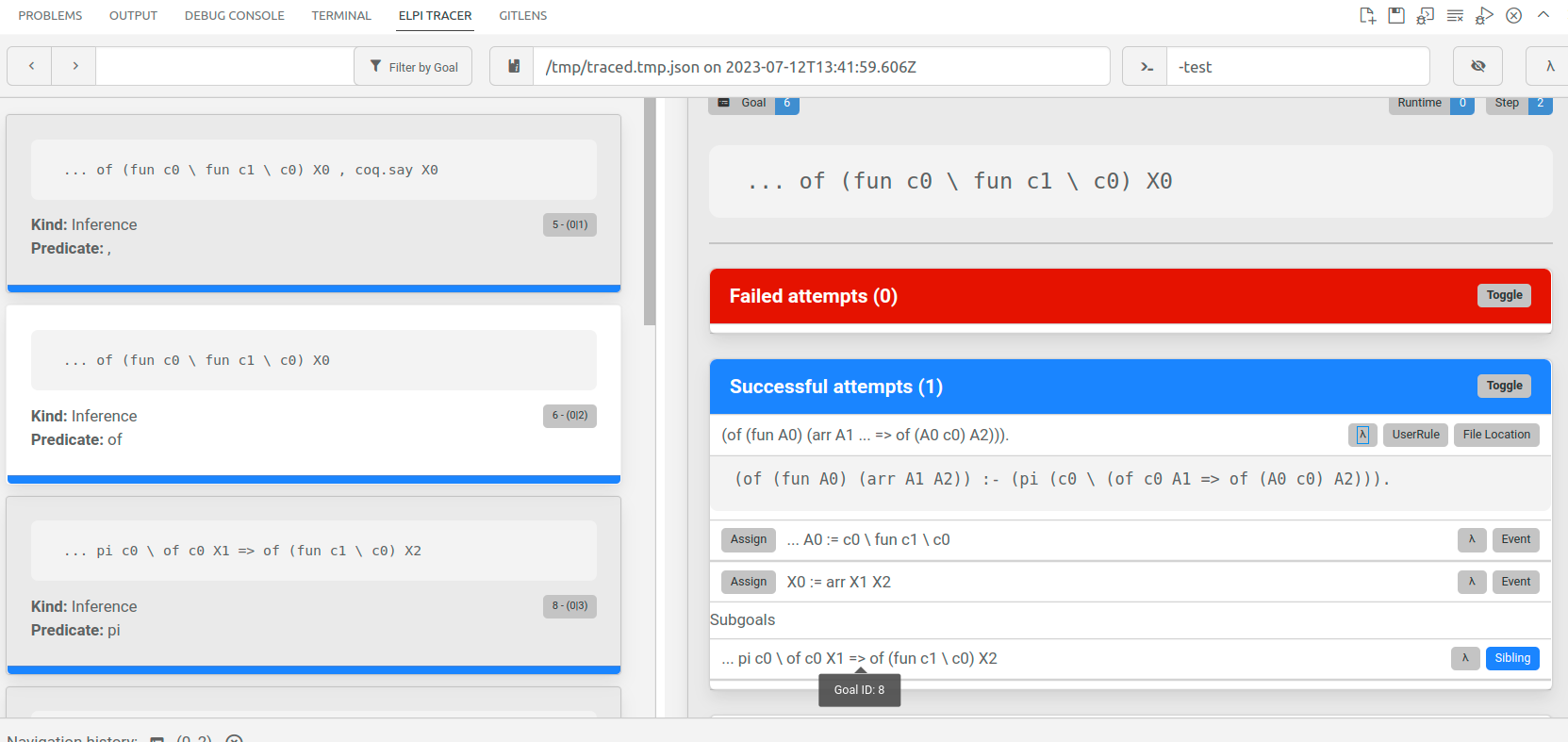
The most sophisticated debugging feature can be used via the Visual Studio Code extension gares.elpi-lang and its Elpi Tracer tab.
Trace browser
In order to generate a trace one needs to execute the Elpi Trace Browser. command and then run any Elpi code.
(* Elpi Trace Browser. *)
The trace file is generated in /tmp/traced.tmp.json. If it does not load automatically one can do it manually by clicking on the load icon, in the upper right corner of the Elpi Tracer panel.
Note
partial display of goals
At the time of writing one may need to disable syntax highlighting in the extension settings in order to get a correct display.
The trace browser displays, on the left column, a list of cards corresponding to a step performed by the interpreter. The right side of the panel gives more details about the selected step. In the image below one can see the goal, the rule being applied, the assignments performed by the unification of the rule's head with the goal, the subgoals generated.
One can also look at the trace in text format (if VSCode is not an option, for example).
Elpi Trace.
The trace can be limited to a range of steps. Look at the numbers run HERE {{{.
Elpi Trace 6 8.
The trace can be limited to a (list of) predicates as follows:
Elpi Trace "of".
One can combine the range of steps with the predicate:
Elpi Trace 6 8 "of".
To switch traces off:
Elpi Trace Off.Good old print
A common λProlog idiom is to have a debug rule
lying around. The :if attribute can be used to
make the rule conditionally interpreted (only if the
given debug variable is set).
Elpi Debug "DEBUG_MYPRED". Elpi Program debug lp:{{ pred mypred i:int. :if "DEBUG_MYPRED" mypred X :- coq.say "calling mypred on " X, fail. mypred 0 :- coq.say "ok". mypred M :- N is M - 1, mypred N. }}.
Printing entire programs
Given that programs are not written in a single place, but rather obtained by accumulating code, Elpi is able to print a (full) program to an text file as follows. The obtained file provides a facility to filter rules by their predicate. Note that the first component of the path is a Coq Load Path (i.e. coqc options -R and -Q), the text file will be placed in the directory bound to it.
Elpi Print stlc "elpi_examples/stlc".Bounding the number of steps
Finally, one can bound the number of backchaining steps performed by the interpreter:
Elpi Query lp:{{ 0 = 0, 1 = 1 }}. Elpi Bound Steps 1.Elpi Bound Steps 0. (* Go back to no bound *)
Pitfalls and tricks
Well, no programming language is perfect.
Precedence of ,, ==> and =>
In this tutorial we only used ==> but Elpi also provides
the standard λProlog implication =>. They have the same meaning
but different precedences w.r.t. ,.
The code a, c ==> d, e reads a, (c ==> (d,e)), that means that
the rule c is available to both d and e.
On the contrary the code a, c => d, e reads a, (c ==> d), e,
making c only available to d.
So, => binds stronger than ,, while ==> binds stronger only
on the left.
According to our experience the precedence of => is a common source
of mistakes for beginners, if only because it is not stable by adding of
debug prints, that is a => b and a => print "doing b", b have
very different meaning (a becomes only available to print!).
In this tutorial we only used ==> that was introduced in Elpi 2.0, but
there is code out there using =>. Elpi 2.0 raises a warning if the
right hand side of => is a conjenction with no parentheses.
A concrete example:
The =!=> operator and functional predicates
When an hypothetical rule is added to a functional predicate the determinacy may fail to detect its mutual exclusiveness, especially if the rule is generated dynamically as below:
X = f P, X ==> q % static error, X could be anything
Elpi 3.0 provides the =!=> connective that adds a tail cut to the
hypothetical rule, be it explicitly given or computed at run time. For example:
(f P :- !) ==> q % fine, new rule for f cuts all the others, f still a function f P =!=> q % desugars to the above (f P :- h P, !) ==> q % fine as before (f P :- h P) =!=> q % desugars to the above X = f P, X =!=> q % at run time it evaluates as below X = f P, X' = (X :- !), X' ==> q X = (f P :- h P), X =!=> q % at run time it evaluates as below X = f P, X' = (X :- h P, !), X' ==> q
Taming backtracking
Backtracking can lead to weird execution traces and bad performances. The main tool to eliminate backtracking is the cut operator, but one may forget to use it. Elpi provides two mechanisms to help with that.
The former one is functional predicates: by declaring a predicate as functional one is typically forced to use cut. This is the recommended way of writing code since Elpi 3.0.
The latter mechanism is the e std.do! predicate that can be used as follows.
pred not-a-backtracking-one. not-a-backtracking-one :- condition, !, std.do! [ step, (generate, test), step, ].
In the example above once condition holds we start a sequence of
steps which we will not reconsider. Locally, backtracking is still
available, e.g. between generate and test.
See also the std.spy-do! predicate which prints each and every step, and the std.spy one which can be used to spy on a single one.
Unification variables v.s. Imperative variables
Unification variables sit in between variables in imperative programming and functional programming. In imperative programming a variable can hold a value, and that value can change over time via assignment. In functional languages variables always hold a value, and that value never changes. In logic programming a unification variable can either be unset (no value) or set to a value that never changes. Backtracking goes back in time, it is not visible to the program.
As a result of this, code like
pred bad-example. bad-example :- X is 1 + 2, X is 4 + 5.
fails, because X cannot be at the same time 3 and 9. Initially
X is unset, then it is set to 3, and finally the programmer is
asserting that 3 (the value hold by X) is equal to 9.
The second call to is does not change the value carried by X!
Unification, and hence the = predicate, plays two roles.
When X is unset, X = v sets the variable.
When X is set to u, X = v checks if the value
of X is equal to u: it is equivalent to u = v.
Further reading
The λProlog website contains useful links to λProlog related material.
Papers and other documentation about Elpi can be found at the Elpi home on github.
Three more tutorials specific to Elpi as an extension language for Coq can be found in the examples folder. You can continue by reading the one about the HOAS for Coq terms.